This Decimal to Binary Converter lets you convert any Decimal number to Binary quickly and easily.
Rate this converter
How to use the Decimal to Binary Converter
Time needed: 1 minute
- Enter the Decimal number
Enter a Decimal Number in the first field.
- Press the Convert button
Press the Convert button below the number field.
- Review the Output
The Binary Number output will appear in the second field.
- Copy or Save
Optionally, you can Copy the output to clipboard, or Save it as a file on your device.
Converter features
| 🔢 Decimal Input length: | Up to 7 digits |
| ⚡ Conversion Speed: | Instant! |
| ➡️ Binary Output: | Display, Copy, Save |
| 🎯 Conversion Accuracy: | 100% |
Read (or watch) our tutorial on How to Convert Decimal to Binary to learn more about the process of converting decimal numbers to binary.
Try the Binary to Decimal Converter too!
How to Convert Decimal to Binary
If you work with computers, you may find yourself needing a basic understanding of the binary number system. Or, maybe you just want to know binary for fun. Either way, understanding how to convert from decimal number system to binary number system can be a useful tool.
Here’s the best part: you don’t need a degree in math or a decimal to binary calculator do it.
Ones and Zeros
You can think of binary as the language computers speak. It is made up by a series of ones and zeros. At first glance, it may look like madness, but there is a method to it. We’ll start with a simple, single-digit, and explain how you can convert a decimal to binary. Let’s use the number 7.
Decimal to binary conversion involves redefining the number you wish to convert. 7 can be represented as simply 7. Or, it can be represented as 4+3. Rewriting the number is the first step in converting to binary. Most importantly, we want to dissect our decimal into the sum of powers of 2.
So let’s look at 7, and let’s consider the powers of 2. What power of 2 is closest to the number 7 while being equal or less than 7?
2² gives us 4, so we’re going to use 4 to start disassembling 7. We must add 3 to make up the rest of 7. So now, we can consider 7=4+3.
It might be helpful to have a table of powers of 2 for reference. We’ve included part of the table in the picture below.

Now we have 3, but there are no powers of 2 that give us 3. We must break down 3 in the same way we did 7. So, find the sum of powers of 2 that will give us 3. Remember, we must begin with powers of 2 equal or less than 3. 2¹ gives us 2, and 20 gives us 1.

We used three different powers of 2 in this example. So, the binary representation of 7 will be three digits long. Since the highest power of 2 we needed was 2², we’re going to start by counting how many times 2² was used. In binary, there can only be two answers to this question: it was used one, or zero times. If we did use it, we’ll indicate it with a 1. If not, we’ll indicate it with a 0.
Using 2² means we’ll mark down a 1. Now, we work down, counting the rest of powers of 2 we used. We used 2¹, so we’ll indicate it with another 1. We used 20, so we’ll use 1 in the final spot.
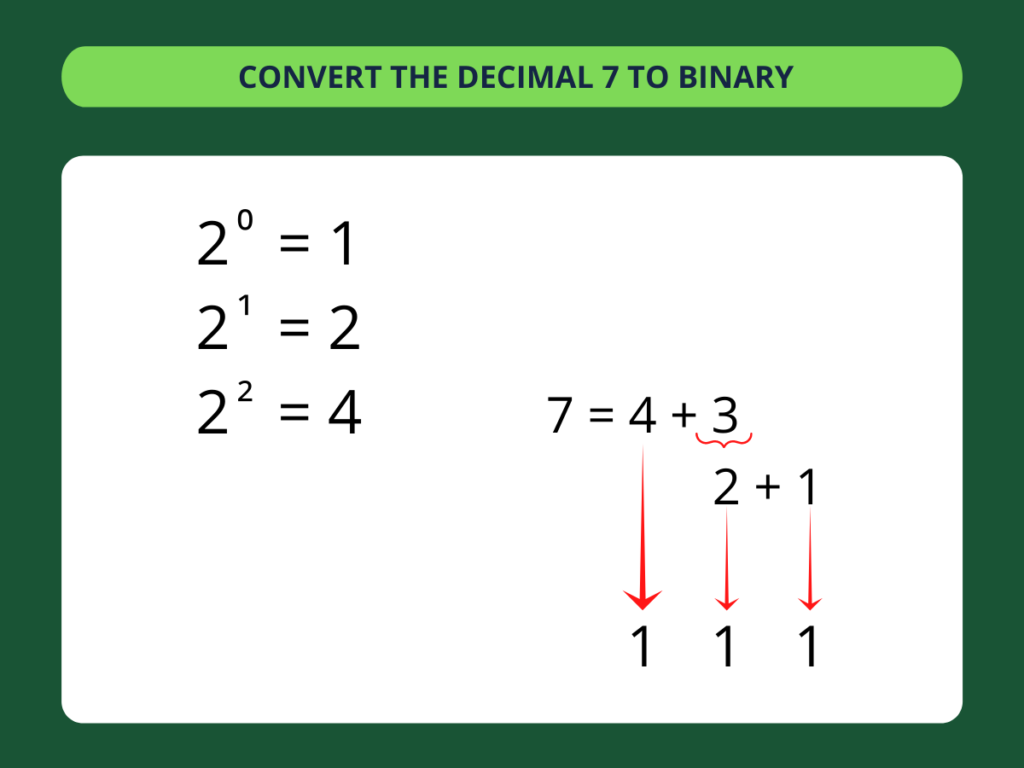
We now have the decimal 7 converted into binary, as 111.
We can use 8 as an even easier example of how to convert decimal to binary. What power of 2 is equal or less than 8? 2³ gives us 8 exactly, so we don’t need to deconstruct anything.
We used 2³ once. We used 2², 2¹, and 20 zero times. So 8 gives us 1000 in binary. Binary is simply counting how many times you used a power of 2 to break down your decimal.

Does that mean if we want to write the decimal 78 in binary, we can combine the binary equivalents in each digit? 111 and 1000? Well, not exactly. 1111000 translates to 120! But if we want to translate 78 to binary, it’s as easy as translating a single decimal value.
Same as before, we’ll look at which power of 2 is closest to 78. 26 gives us 64, which is the closest to 78 we can find without going over 78. We can redefine 78 as 78 = 64 + 14.

Now we must redefine 14 as well. We can use 2³ to give us 8, and now we need to add 6 to make 14. Since 6 isn’t an exponent of 2 either, it needs to be deconstructed into a sum of powers of 2.
Lucky for us, 2² gives us 4, and 2¹ gives us 2. Now, no more numbers need to be deconstructed, and we can turn it into binary. Since we started all the way at 26 we must ask if we used that power, and each one that came before it, back to 20.
How many times did we use 26? 1
How many times did we use 25? 0
How many times did we use 24? 0
How many times did we use 2³? 1
How many times did we use 2²? 1
How many times did we use 2¹? 1
How many times did we use 20? 0
So, 78 in binary is 1001110

Not as scary as you thought, right? The same algorithm works for three digit decimals and upwards. The only difference is you might need a more extensive table of powers of 2 (or a calculator) in order to work through the equation. Or, you can use a decimal to binary converter for larger numbers, like the one at the top of this page. Bottom line; converting decimal to binary is as easy as 1, 2, 3 – or shall we say, 1, 10, 11!
Table of the First hundred Decimal numbers in Binary
For your convenience, the following table shows the decimal numbers from 0 to 100 along with their Binary representation.
| Decimal | Binary |
| 0 | 0 |
| 1 | 1 |
| 2 | 10 |
| 3 | 11 |
| 4 | 100 |
| 5 | 101 |
| 6 | 110 |
| 7 | 111 |
| 8 | 1000 |
| 9 | 1001 |
| 10 | 1010 |
| 11 | 1011 |
| 12 | 1100 |
| 13 | 1101 |
| 14 | 1110 |
| 15 | 1111 |
| 16 | 10000 |
| 17 | 10001 |
| 18 | 10010 |
| 19 | 10011 |
| 20 | 10100 |
| 21 | 10101 |
| 22 | 10110 |
| 23 | 10111 |
| 24 | 11000 |
| 25 | 11001 |
| 26 | 11010 |
| 27 | 11011 |
| 28 | 11100 |
| 29 | 11101 |
| 30 | 11110 |
| 31 | 11111 |
| 32 | 100000 |
| 33 | 100001 |
| 34 | 100010 |
| 35 | 100011 |
| 36 | 100100 |
| 37 | 100101 |
| 38 | 100110 |
| 39 | 100111 |
| 40 | 101000 |
| 41 | 101001 |
| 42 | 101010 |
| 43 | 101011 |
| 44 | 101100 |
| 45 | 101101 |
| 46 | 101110 |
| 47 | 101111 |
| 48 | 110000 |
| 49 | 110001 |
| 50 | 110010 |
| 51 | 110011 |
| 52 | 110100 |
| 53 | 110101 |
| 54 | 110110 |
| 55 | 110111 |
| 56 | 111000 |
| 57 | 111001 |
| 58 | 111010 |
| 59 | 111011 |
| 60 | 111100 |
| 61 | 111101 |
| 62 | 111110 |
| 63 | 111111 |
| 64 | 1000000 |
| 65 | 1000001 |
| 66 | 1000010 |
| 67 | 1000011 |
| 68 | 1000100 |
| 69 | 1000101 |
| 70 | 1000110 |
| 71 | 1000111 |
| 72 | 1001000 |
| 73 | 1001001 |
| 74 | 1001010 |
| 75 | 1001011 |
| 76 | 1001100 |
| 77 | 1001101 |
| 78 | 1001110 |
| 79 | 1001111 |
| 80 | 1010000 |
| 81 | 1010001 |
| 82 | 1010010 |
| 83 | 1010011 |
| 84 | 1010100 |
| 85 | 1010101 |
| 86 | 1010110 |
| 87 | 1010111 |
| 88 | 1011000 |
| 89 | 1011001 |
| 90 | 1011010 |
| 91 | 1011011 |
| 92 | 1011100 |
| 93 | 1011101 |
| 94 | 1011110 |
| 95 | 1011111 |
| 96 | 1100000 |
| 97 | 1100001 |
| 98 | 1100010 |
| 99 | 1100011 |
| 100 | 1100100 |
Questions and Answers about Decimal to Binary conversion
The Decimal to Binary Converter at ConvertBinary.com is really easy to use.
Just follow these steps: enter your decimal number in the first field, then push the “Convert” button.
The binary representation for your decimal number will immediately appear in the field below.
To convert decimal numbers to their binary equivalent, you have two options: you can either use an online converter (like the one provided for free by ConvertBinary.com), or you can do it manually.
If you want to learn how to convert decimal to binary manually, you can read this guide, or watch the associated tutorial.
It takes the decimal number, and considers the powers of 2. It finds the power of 2 that is closest to the decimal, while being equal or less than the decimal itself.
Then it iterates the process until there’s no remainder left.
The process is automatic and so quick that it feels like it’s instant, even for large numbers.
Of course! If you want to convert any number represented in binary to its decimal equivalent, you can use the Binary to Decimal Converter at ConvertBinary.com.
The number 10 (Ten) is 1010 (one-zero-one-zero) in Binary.
You can find a table of the binary representations of decimal numbers from 0 to 100 at ConvertBinary.com.
